In statistics, an estimator is a function that associates a parameter estimate to each possible sample we can observe.
In an estimation problem, we need to choose a
parameter
![[eq1]](/images/estimator__1.png){kind=small}
from
a set
.
We do so by using a set of observations from an unknown probability distribution.
The set of observations is called a sample and it is denoted by
.
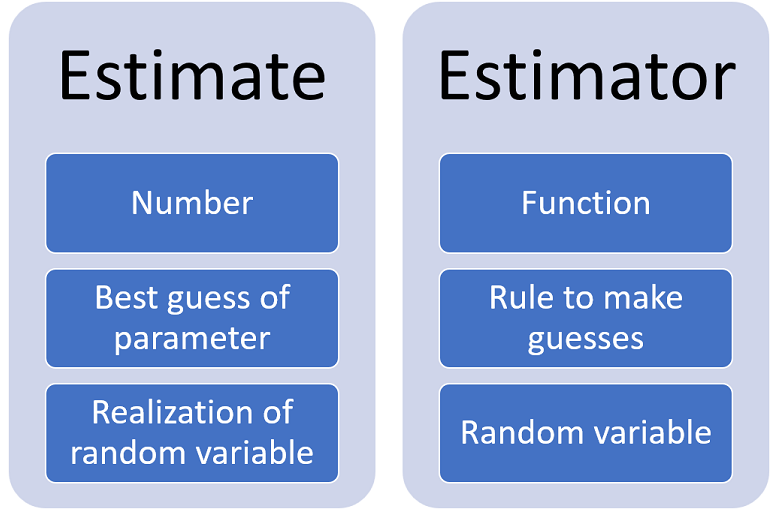
The chosen
is our best guess of the true and unknown parameter
,
which characterizes the probability distribution that generated the sample.
The parameter
is called an estimate of
.
When
is chosen by using a predefined rule that associates an estimate
to each possible sample
,
we can write
as a function of
:![[eq2]](/images/estimator__13.png){kind=small}
The function
![[eq3]](/images/estimator__14.png){kind=small}
is called an estimator.
The sample
,
before being observed, is regarded as randomly drawn from the distribution of
interest. Therefore, the estimator
,
being a function of
,
is regarded as a
random variable.
After the sample
is observed, the
realization
of the estimator is called an estimate of the true parameter
.
In other words, an estimate is a realization of an estimator.
A function of a sample
is called a statistic.
Therefore, an estimator
is a statistic.
However, not all statistics are estimators. For example, the z-statistic often used in hypothesis tests about the mean is not an estimator.
Commonly found examples of estimators are:
the sample mean, used to estimate the expected value of an unknown distribution;
the sample variance, utilized to estimate the variance of an unknown distribution;
the OLS estimator of the vector of regression coefficients in a linear regression model;
the maximum likelihood estimator of the parameters of a probability density or probability mass function;
Different estimators of the same parameter are often compared by looking at their mean squared error (MSE).
The MSE is equal to the expected value of the squared difference between the
estimator and the true value of the
parameter:![[eq6]](/images/estimator__23.png){kind=small}
The square provides a measure of the distance between the estimator and the true value.
Therefore, the lower the MSE is, the lower on average the distance of the estimator from the true value, and the better the estimator is.
For an example of such comparisons, see the lecture on Ridge estimation.
The MSE is only one of the metrics used to assess estimators.
There are also other metrics, such as the mean absolute error
(MAE):![[eq7]](/images/estimator__24.png){kind=small}
These metrics are known as loss
functions, which quantify the loss generated by the difference between the
estimate
and the true value
.
When is an estimator considered well-behaved and reliable?
Besides a small MSE, the following two properties are often deemed desirable:
unbiased estimator: an estimator
whose expected value is equal to the true parameter
;
consistent estimator: an
estimator that converges to
as the sample size gets large.
Until now we have discussed point estimators, that is, rules used to produce our best guess of a parameter value.
That best guess is a single number, or a vector of numbers.
There are also interval estimators (also called set estimators) which give us intervals of numbers that contain the true parameter value with high probability.
The intervals of numbers are called confidence intervals or confidence sets.
To know more about interval estimators and their properties, you can consult the page on set estimators.
More details about estimators can be found in the lecture entitled Point estimation, which discusses the concept of estimator and the main criteria used to evaluate estimators.
Previous entry: Distribution function
Next entry: Event
Please cite as:
Taboga, Marco (2021). "Estimator", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/estimator.
Most of the learning materials found on this website are now available in a traditional textbook format.
