An event is a subset of the set of all possible outcomes of a probabilistic experiment.
The concept of event is fundamental in probability theory. In fact, whenever we speak about probability, we explicitly or implicitly refer to the probability of an event.
The set of all possible outcomes is called
sample space and it is usually denoted
by
.
Thus, an event
is a subset of
,
which is indicated
bywhere
is the inclusion symbol.
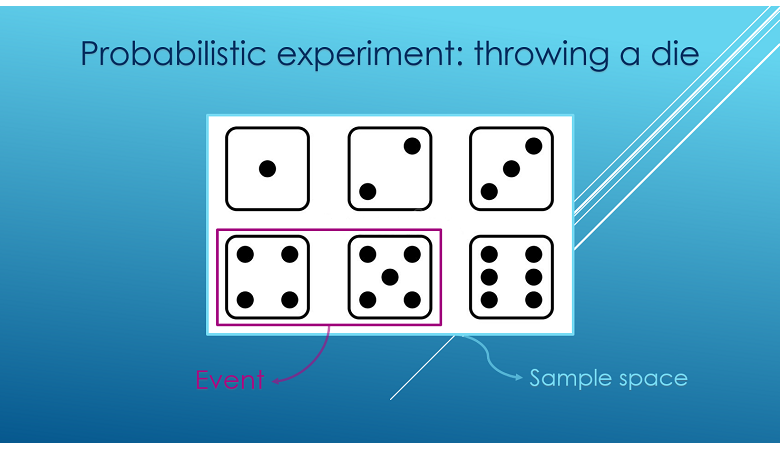
If the probabilistic experiment is the roll of a die, the set of all possible
outcomes
is![[eq2]](/images/event__6.png){kind=small}
In this setting, three instances of events
are![[eq3]](/images/event__7.png)
The event
could be described in words as "An odd number appears face up".
The event
could be described as "A number strictly greater than four appears face up".
The event
could be described as "The number
appears face up".
In case you are wondering about the curly-bracket notation, you are strongly advised to revise the introductory lecture on set theory, where we explain how the notation is used.
In a probabilistic model, each event
is assigned a probability
,
which measures how likely it is that
will happen.
Example
If, as in the above example, the probabilistic experiment is the roll of a
die, we could
have![[eq5]](/images/event__15.png){kind=small}
and
![[eq6]](/images/event__16.png){kind=small}
In
other words, the probabilities of the events
and
are one and two sixths, respectively.
There are some events that have special names.
A sure event is an event that always happens. It coincides with the set of all possible outcomes.
If we employ the same notation used above,
is the sure event.
In the roll-of-a-die example, the sure event
could be described in words as "Any one of the numbers from 1 to 6 appears
face up".
An impossible event is an event that never happens. It coincides with the
empty set
.
You can find a careful discussion of this apparently strange definition in the glossary entry on impossible events.
When we compute probabilities, we often deal with the union of two or more events.
The union of two events
and
is itself an event. It comprises all the outcomes that belong to
or to
.
In the above example, we
had![[eq7]](/images/event__26.png)
Then, the union of
and
,
denoted by
,
is![[eq8]](/images/event__30.png){kind=small}
The intersection of
and
is the event that comprises all the outcomes that belong both to
and to
.
If
and
are defined as above, then the intersection of
and
,
denoted by
,
is![[eq9]](/images/event__40.png){kind=small}
Two events are said to be mutually exclusive if their intersection is equal to the empty set.
For example,
![[eq10]](/images/event__41.png){kind=small}
andare
mutually exclusive
because
In simple probabilistic settings, all subsets of the sample space
are considered events. However, there are also more complicated settings in
which some subsets of
cannot be considered events. In those complicated settings, the sets that can
be considered events are called measurable sets (see the
lecture on Probability).
For other examples and more detailed explanations of the concept of event, you can go to the lecture entitled Probability.
Moreover, you might be interested in the following more advanced concepts:
Previous entry: Estimator
Next entry: Factorial
Please cite as:
Taboga, Marco (2021). "Event", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/event.
Most of the learning materials found on this website are now available in a traditional textbook format.
