This is an introduction to the fundamental concepts of probability theory. Each lecture contains detailed proofs and derivations of all the main results, as well as solved exercises.
Events having zero probability, almost sure events, almost sure properties
Sample space, sample points, events, probability and its fundamental properties
Prior probability, posterior probability, updating
How to revise probabilities when new information arrives
Definition and explanation of independence and mutual independence
Joint distributions, marginal distributions
Discrete and continuous random variables, probability mass and density functions
Expected value and the Lebesgue integral
A rigorous definition of expected value, based on the theory of Lebesgue integration
The mean of a random variable, how to compute it, its properties
Dispersion around the mean, definition, interpretation, fundamental properties
Properties of the expected value
Linearity of the expected value, expectation of positive random variables, other properties
Another measure of association between random variables
Association between random variables, definition, interpretation, properties
Equal to one when an event happens and zero otherwise
A multivariate generalization of the concept of variance
Cut-off point of a distribution that leaves to its left a given proportion of the distribution
Conditional probability distributions
How to update the distribution of a random variable after receiving some information
Rigorous conditional probability
A more rigorous presentation of conditional probability based on the theory of sigma-algebras
Definition and characterization of independence between random variables
How to compute the expected value of a random variable after observing the value of another
A fundamental inequality derived from Markov's inequality
Provides an upper bound to the probability that a random variable will exceed a threshold
Concerns the expected value of convex and concave transformations of a random variable
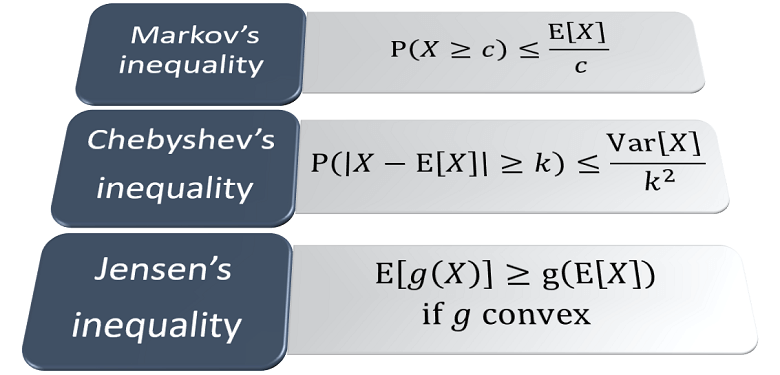
Legitimate probability density functions
Properties of probability density functions and how to construct them
Legitimate probability mass functions
Properties of probability mass functions and how to construct them
Factorization into marginal and conditional probability density function
Factorization into marginal and conditional probability mass function
How to derive the joint distribution of a function of a random vector
How to derive the distribution of Y=g(X) from the distribution of X
Sums of independent random variables
How to derive the distribution of a sum from the distributions of the summands
Definition of cross-moment and central cross-moment of a random vector
Definition of moment and central moment of a random variable
Joint moment generating function
Generalizes the concept of moment generating function to random vectors
Definition, computation of moments, characterization of distributions
Generalizes the concept of characteristic function to random vectors
Definition, computation of moments, characterization of distributions
The logarithm of the moment generating function has some interesting properties
A measure of the dissimilarity between two probability distributions
200 probability questions to check your knowledge of probability theory
Most of the learning materials found on this website are now available in a traditional textbook format.