StatLect offers one of the largest collections of probability exercises and problem sets.
The exercises are subdivided by topic. For each topic you will find:
A table that contains links to problem sets with solved exercises.
Some review questions. They help you understand whether you know the theory that is needed to solve the exercises. You can safely skip the questions tagged as advanced if you are taking a first course in probability.
| Problem sets | Number of solved exercises |
|---|---|
| Probability | 3 |
| Zero-probability events | 2 |
Can you explain in simple words the main elements of a probabilistic experiment?
What are a sample space, a possible outcome, a realized outcome?
What is an event?
What is the probability of an event?
What properties does probability need to satisfy?
How do you compute the probability of the union of two events?
How do you compute the probability of the complement of a given event?
What is the probability of the empty set?
What is the probability of the sure event?
Can you explain the monotonicity property of probability?
What is a zero-probability event?
Is a zero-probability event an event that never happens?
Can you give a rigorous definition of probability?
What is a space of events?
What is a sigma-algebra?
What is a probability space?
What is sigma-additivity?
What is countable additivity?
What is an almost sure event?
When does a property hold almost surely?
Do you know the meaning of the acronyms a.s. and w.p.1?
| Problem sets | Number of solved exercises |
|---|---|
| Conditional probability | 3 |
| Bayes' rule | 3 |
| Independent events | 3 |
Can you intuitively define the concept of conditional probability?
What is the conditional probability of an event A given another event B?
What formula can be used to compute conditional probabilities?
Can the formula be used in any case? When is it not possible to apply the formula?
What is the 'Law of total probability'?
What is Bayes' rule?
Can you name the quantities involved in Bayes' rule?
What is a prior probability?
What is a posterior probability?
Can you give a definition of independent events?
What is the relation between the concept of independence and that of conditional probability?
What are mutually independent events?
What are jointly independent events?
Can you prove the formula for conditional probability when all sample points are equally likely?
Can you prove Bayes' rule?
What are the main obstacles to giving a completely general definition of conditional probability?
Is mutual independence a stronger property than pairwise independence?
| Problem sets | Number of solved exercises |
|---|---|
| Random variables | 6 |
| Probability mass function | No problem sets / 1 example |
| Probability density function | No problem sets / 1 example |
| Cumulative distribution function | No problem sets / 1 example |
What is a random variable?
Do you understand the definition of random variable as a function defined on a sample space?
What is a realization of a random variable?
What is the support (or range) of a random variable?
Can you define the concept of a discrete random variable?
Can the support of a discrete random variable have infinitely many elements?
What is the probability mass function (pmf) of a random variable?
What properties does the pmf satisfy?
Can you make an example of a discrete random variable?
What is a continuous random variable?
What are the main differences between discrete and continuous random variables?
What is the probability density function (pdf) of a random variable?
How do you interpret the value taken by the pdf at a given point?
How is the pdf used to derive the probability of a given interval?
What properties does the pdf satisfy?
Can you make an example of a continuous random variable?
Are there random variables that are neither discrete nor continuous?
Is there a general way to characterize the distribution of a random variable?
What is a (cumulative) distribution function (cdf)?
How do you use the cdf to compute the probability of an interval?
What do you obtain if you take the first derivative of the cdf of a continuous variable?
Do you recognize the plot below?
What is the blue line?
What is the red region?
How can you compute the area of the red region?
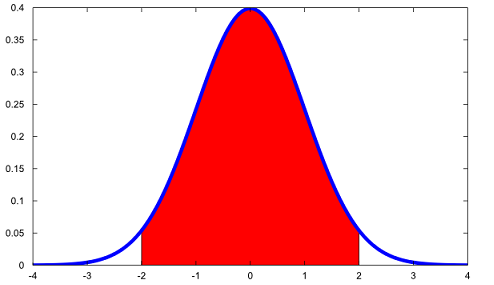
What properties does a cdf satisfy?
What is a Borel sigma-algebra?
Can you give a completely rigorous definition of random variable?
| Problem sets | Number of solved exercises |
|---|---|
| Random vectors | 6 |
| Conditional probability distributions | 3 |
| Independent random variables | 3 |
What is a random vector?
How do the concepts of discrete and continuous random variable generalize to random vectors?
What are the joint probability mass function and the joint probability density function?
What is the joint (cumulative) distribution function of a random vector?
What is a marginal distribution?
What are the marginal pmf, pdf and cdf?
How can they be derived from the joint pmf, pdf and cdf?
What is a conditional probability distribution?
What are the conditional pmf, pdf and cdf?
What are the relationships between joint, marginal and conditional pmf, pdf and cdf?
Can you define the concept of independence between random variables?
Can you explain it intuitively?
How can you check whether two random variables are independent?
Is there a general way to check independence?
How can you check whether two discrete variables are independent?
How can you check whether two continuous variables are independent?
Can you define mutual independence among random variables?
How can we use expected values to check mutual independence?
| Problem sets | Number of solved exercises |
|---|---|
| Expected value | 6 |
| Properties of the expected value | 3 |
| Conditional expectation | 3 |
| Expected value and the Lebesgue integral (advanced) | N/A |
What is the expected value (or mean) of a random variable?
How do you compute the expected value of a discrete random variable?
How do you compute the expected value of a continuous random variable?
Is the expected value always defined?
Under what conditions is it defined?
What is the transformation theorem (also called 'Law of the unconscious statistician', or LOTUS)?
Are you familiar with the main properties of the expected value?
How do you compute the expected value of a sum of random variables?
How do you compute the expected value of a linear transformation of a random variable?
How do you compute the expected value of a linear combination of random variables?
How is the expected value of a random vector defined?
What is the conditional expectation (or conditional expected value)?
How do you compute it?
What properties does it enjoy?
What is the 'Law of iterated expectations'?
How do you compute the expected value of a random variable that is neither discrete nor continuous?
Can you use the Stieltjes integral to define the expected value?
Can you give a rigorous definition of expected value?
Can you use the Lebesgue integral to define the expected value?
When is a random variable said to be integrable?
What are Lp spaces?
| Problem sets | Number of solved exercises |
|---|---|
| Variance | 6 |
| Covariance matrix | 3 |
| Moments | No problem sets / 2 examples |
| Cross-moments | No problem sets / 2 examples |
How is variance defined?
Is it always well-defined?
What is the interpretation of variance?
Do you know a formula that often facilitates the computation of variance?
How do you compute the variance of a discrete random variable?
How do you compute the variance of a continuous random variable?
What happens to the variance of a random variable if you add a constant to that variable?
What happens to the variance of a random variable if you multiply that variable by a constant?
What is the relationship between variance and standard deviation?
How does the concept of variance generalize to random vectors?
What is a covariance matrix?
What is a variance-covariance matrix?
What are the diagonal elements of a covariance matrix?
What are the off-diagonal elements of a covariance matrix?
What happens to the covariance matrix of a random vector when you perform linear transformations of that vector?
What is the n-th moment of a random variable?
What is the n-th central moment of a random variable?
What is the n-th cross moment of a random vector?
What is the n-th central cross-moment of a random vector?
What is a square integrable random variable?
| Problem sets | Number of solved exercises |
|---|---|
| Covariance | 6 |
| Linear correlation | 3 |
| Independent random variables | 3 |
How is covariance defined?
Is it always well-defined?
What is its interpretation?
What formula often simplifies the calculation of covariance?
How do you compute the covariance between two discrete random variables?
How do you compute the covariance between two continuous random variables?
What properties does covariance enjoy?
Why is covariance symmetric?
What is the bilinearity of covariance?
How do you compute the variance of a sum of two random variables?
If two random variables have zero covariance, are they independent?
If two random variables are independent, is their covariance equal to zero?
What is the linear correlation coefficient between two random variables?
Why is the linear correlation coefficient easier to interpret than the covariance?
What are the bounds of the linear correlation coefficient?
If you know the linear correlation coefficient between two variables, is that sufficient to characterize their statistical dependence?
| Problem sets | Number of solved exercises |
|---|---|
| Markov's inequality | 1 |
| Chebyshev's inequality | 1 |
| Jensen's inequality | 1 |
What is Markov's inequality?
What is Chebyshev's inequality?
What is Jensen's inequality?
What can you say about the expected value of a convex function of a random variable?
What can you say about the expected value of a concave function of a random variable?
What can you say about the expected value of a strictly convex function of a random variable?
What can you say about the expected value of a strictly concave function of a random variable?
Are you able to prove Chebyshev's inequality?
| Problem sets | Number of solved exercises |
|---|---|
| Functions of random variables | 3 |
| Functions of random vectors | 2 |
| Sums of independent random variables | 2 |
Given the pdf of a continuous variable X, how do you derive the pdf of a function g(X)?
Is there a simple formula to do so?
Under what conditions can it be used?
Given the pmf of a discrete variable X, how do you derive the pmf of a function g(X)?
Is there a simple formula to do so?
Under what conditions can it be used?
How can we derive the distribution of a function of a random vector?
What is a Jacobian?
How do you compute the distribution of a sum of independent random variables?
What is a convolution?
Can you derive the cdf of a function g(X) of a random variable X?
| Problem sets | Number of solved exercises |
|---|---|
| Moment generating function | 3 |
| Joint moment generating function | 3 |
| Characteristic function | 3 |
| Joint characteristic function | 3 |
What is the moment generating function (mgf) of a random variable?
Does it always exist?
How is it used to derive the moments of a random variable?
Why do we say that the mgf completely characterizes the distribution of a random variable?
If two variables have the same mgf, do they have the same distribution?
Why is the mgf so useful?
If you take a linear transformation of a random variable, how does its mgf change?
What is the mgf of a sum of independent variables?
How does the concept of mgf generalize to random vectors?
What is the characteristic function (cf) of a random variable?
Does it always exist?
Can you say what are the similarities and differences between the cf and the mgf?
How does the concept of cf generalize to random vectors?
If you know the characteristic function of a random variable, how can you tell whether the n-th moment of that variable exists or not?
Please cite as:
Taboga, Marco (2021). "Probability exercises and questions", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/probability-questions.
Most of the learning materials found on this website are now available in a traditional textbook format.