The Poisson distribution is a discrete probability distribution used to model the number of occurrences of a random event.
Suppose that an event can occur several times within a given unit of time.
When the total number of occurrences of the event is unknown, we can think of it as a random variable.
This random variable has a Poisson distribution if the time elapsed between two successive occurrences of the event:
has an exponential distribution;
it is independent of previous occurrences.
A classical example of a random variable having a Poisson distribution is the number of phone calls received by a call center.
If the time elapsed between two successive phone calls has an exponential distribution and it is independent of the time of arrival of the previous calls, then the total number of calls received in one hour has a Poisson distribution.
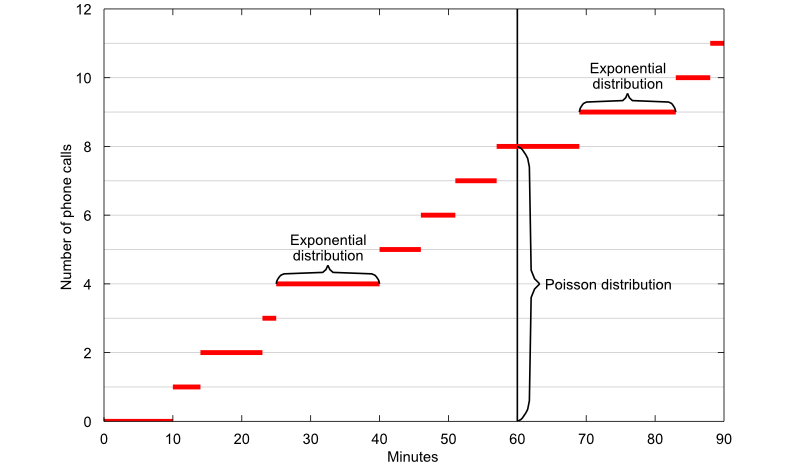
The concept is illustrated by the plot above, where the number of phone calls received is plotted as a function of time:
the graph of the function makes an upward jump each time a phone call arrives;
the time elapsed between two successive phone calls is equal to the length of each horizontal segment and it has an exponential distribution;
the number of calls received in 60 minutes is equal to the length of the segment highlighted by the vertical curly brace and it has a Poisson distribution.
A Poisson random variable is characterized as follows.
Definition
Let
be a discrete random
variable. Let its
support be the set
of non-negative integer
numbers:
Let
.
We say that
has a Poisson distribution with parameter
if its probability mass
function
is
where
is the factorial of
.
The relation between the Poisson distribution and the exponential distribution is summarized by the following proposition.
Proposition
The number of occurrences of an event within a unit of time has a Poisson
distribution with parameter
if the time elapsed between two successive occurrences of the event has an
exponential distribution with parameter
and it is independent of previous occurrences.
Denote by
the number of occurrences of the event and
by
![[eq4]](/images/Poisson-distribution__12.png) Note
that there are at least
Note
that there are at least
occurrences of the event (i.e.,
)
within a unit of time if and only if the sum of the times elapsed between the
occurrences is less than one unit of time. In other words, the events
and
coincide.
Therefore,
for
any
.
Thus, the distribution of
can be derived from the distribution of the waiting times
.
We are going to prove that the assumption that the waiting times are
exponential implies that
has a Poisson distribution. Denote by
the sum of waiting
times:
Since
the sum of independent exponential random
variables with common parameter
is a Gamma random variable with parameters
and
,
then
is a Gamma random variable with parameters
and
,
i.e., its probability
density function
is
where
and
the last equality stems from the fact that we are considering only integer
values of
.
We need to integrate the density function to compute the probability that
is less than
:
The
last integral can be computed integrating by parts
times:
![[eq13]](/images/Poisson-distribution__38.png) Multiplying
by
Multiplying
by
,
we
obtain
Thus,
we have
obtained
![[eq15]](/images/Poisson-distribution__41.png) But
this is exactly what we get when
But
this is exactly what we get when
has a Poisson
distribution:
The expected value of a Poisson random variable
is
It
can be derived as
follows:![[eq18]](/images/Poisson-distribution__46.png)
The variance of a Poisson random variable
is
It
can be derived thanks to the usual
variance formula
():
![[eq21]](/images/Poisson-distribution__50.png)
The moment generating function of a Poisson
random variable
is defined for any
:
By
using the definition of moment generating function, we
getwhere
is
the usual Taylor series expansion of the exponential function. Furthermore,
since the series converges for any value of
,
the moment generating function of a Poisson random variable exists for any
.
The characteristic function of a Poisson random
variable
is
By
using the definition of characteristic function, we
obtainwhere
is
the usual Taylor series expansion of the exponential function (note that the
series converges for any value of
).
The distribution function
of a Poisson random variable
is
where
is
the floor of
,
i.e. the largest integer not greater than
.
By using the definition of distribution
function, we
get![[eq30]](/images/Poisson-distribution__68.png)
Values of
are usually computed by computer algorithms. For example, the MATLAB command:
poisscdf(x,lambda)
returns the value of the distribution function at the point
x when the parameter of the distribution is equal to
lambda.
Below you can find some exercises with explained solutions.
The time elapsed between the arrival of a customer at a shop and the arrival of the next customer has an exponential distribution with expected value equal to 15 minutes. Furthermore, it is independent of previous arrivals.
What is the probability that more than 6 customers arrive at the shop during the next hour?
If a random variable has an exponential
distribution with parameter
,
then its expected value is equal to
.
Here
Therefore,
.
If inter-arrival times are independent exponential random variables with
parameter
,
then the number of arrivals during a unit of time has a Poisson distribution
with parameter
.
Thus, the number of customers that will arrive at the shop during the next
hour (denote it by
)
is a Poisson random variable with parameter
.
The probability that more than 6 customers arrive at the shop during the next
hour
is
![[eq33]](/images/Poisson-distribution__78.png) and
the value of
and
the value of
can be calculated with a computer algorithm, for example with the MATLAB
command
At a call center, the time elapsed between the arrival of a phone call and the arrival of the next phone call has an exponential distribution with expected value equal to 15 seconds. Furthermore, it is independent of previous arrivals.
What is the probability that less than 50 phone calls arrive during the next 15 minutes?
If a random variable has an exponential
distribution with parameter
,
then its expected value is equal to
.
Here
where,
in the last equality, we have taken 15 minutes as the unit of time. Therefore,
.
If inter-arrival times are independent exponential random variables with
parameter
,
then the number of arrivals during a unit of time has a Poisson distribution
with parameter
.
Thus, the number of phone calls that will arrive during the next 15 minutes
(denote it by
)
is a Poisson random variable with parameter
.
The probability that less than 50 phone calls arrive during the next 15
minutes
is
![[eq37]](/images/Poisson-distribution__89.png) and
the value of
and
the value of
can be calculated with a computer algorithm, for example with the MATLAB
command
poisscdf(49,60)
Please cite as:
Taboga, Marco (2021). "Poisson distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/Poisson-distribution.
Most of the learning materials found on this website are now available in a traditional textbook format.