In this lecture we introduce and discuss the notion of quantile of the probability distribution of a random variable.
At the end of the lecture, we report some quantiles of the normal distribution, which are often used in hypothesis testing.
We start with an informal definition.
The
-quantile
of a random
variable
is a value, denoted by
,
such that:
with probability
;
with probability
.
Thus, the quantile
is a cut-off point that divides the
support of
in two parts:
the part to the left of
,
which has probability
;
the part to the right of
,
which has probability
.
There are important cases in which the informal definition works perfectly well. However, there are also many cases in which it is flawed. Let us see why.
In the above definition, we require
that
Remember that the distribution
function
of a random variable
is defined
as
Therefore, we are asking
that
However, we know that the distribution function may be discontinuous. In other
words, it may jump and it may not take all the values between
and
.
As a consequence, there may not exist a value
that satisfies equation (1). The distribution function may jump from a value
lower than
to a value higher than
without ever being equal to
.
The lack of existence of a solution to equation (1) is not the only problem.
In fact, not only the distribution function may jump, but it may also be flat over some intervals.
In other words, there may be more that one value of
that satisfies equation (1).
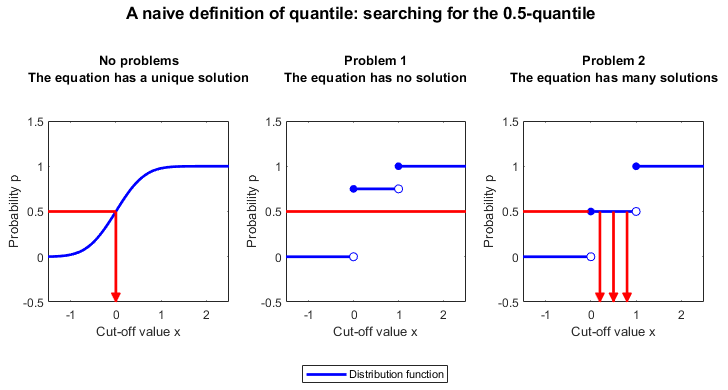
How do we solve the two problems with the informal definition?
We start from problem 2: equation (1) may have more than one solution.
We could solve the problem by always choosing the smallest
solution:![]()
But this would leave problem 1 unsolved: since equation (1) may have no
solution, the
setmay
be empty.
To solve both problems, we minimize over the larger set
Since any distribution function
converges to
as
goes to infinity, the latter set is never empty (provided that
).
Therefore, we define the quantile
as![]()
What we have said can be summarized in the following formal definition.
Definition
Let
be a random variable having distribution function
.
Let
.
The
-quantile
of
,
denoted by
is
![]()
We have imposed the condition
because:
if
,
then
![]()
if
,
then the
set
![]() may
be empty, as, for example, in the important case in which
may
be empty, as, for example, in the important case in which
has a normal distribution.
Let us make an example.
Let
be a discrete random
variable with
support
and
probability mass
function
![[eq26]](/images/quantile__51.png)
The distribution function of
is
![[eq27]](/images/quantile__53.png)
Suppose that we want to compute the
-quantile
for
.
There is no
such
that
However, the smallest
such that
is
because
for
and
for
.
Thus, we
have
When
is regarded as a function of
,
that is,
,
it is called quantile function.
The quantile function is often denoted
by
When the distribution function is continuous and strictly increasing on
,
then the smallest
that
satisfies
is
the unique
that
satisfies
Furthermore, the distribution function has an inverse function
and we can
write
In this case, the quantile function coincides with the inverse of the
distribution
function:
Example
If a random variable
has a standardized Cauchy distribution, then its distribution function
is
![]() which
is a continuous and strictly increasing function. The
which
is a continuous and strictly increasing function. The
-quantile
of
is
![]()
Some quantiles have special names:
if
,
then the quantile
is called median;
if
(for
),
then the quantiles are called quartiles
(
is the first quartile,
is the second quartile and
is the third quartile);
if
(for
),
then the quantiles are called deciles
(
is the first decile,
is the second decile and so on);
if
(for
),
then the quantiles are called percentiles
(
is the first percentile,
is the second percentile and so on).
Some quantiles of the standard normal distribution (i.e., the normal distribution having zero mean and unit variance) are often used as critical values in hypothesis testing.
The quantile function of a normal distribution is equal to the inverse of the distribution function since the latter is continuous and strictly increasing.
However, as we explained in the lecture on normal distribution values, the distribution function of a normal variable has no simple analytical expression.
Therefore, the quantiles of the normal distribution need to be looked up in a table or calculated with a computer algorithm.
We report in the table below some of the most commonly used quantiles.
| Name of quantile | Probability p | Quantile Q(p) |
|---|---|---|
| First millile | 0.001 | -3.0902 |
| Fifth millile | 0.005 | -2.5758 |
| First percentile | 0.010 | -2.3263 |
| Twenty-fifth millile | 0.025 | -1.9600 |
| Fifth percentile | 0.050 | -1.6449 |
| First decile | 0.100 | -1.2816 |
| First quartile | 0.250 | -0.6745 |
| Median | 0.500 | 0 |
| Third quartile | 0.750 | 0.6745 |
| Ninth decile | 0.900 | 1.2816 |
| Ninety-fifth percentile | 0.950 | 1.6449 |
| Nine-hundredth and seventy-fifth millile | 0.975 | 1.9600 |
| Ninety-ninth percentile | 0.990 | 2.3263 |
| Nine-hundredth and ninety-fifth millile | 0.995 | 2.5758 |
| Nine-hundredth and ninety-ninth millile | 0.999 | 3.0902 |
The above definition of quantile of a distribution is the most common one in probability theory and mathematical statistics.
However, there are also other slightly different definitions. For a review, see https://mathworld.wolfram.com/Quantile.html.
Please cite as:
Taboga, Marco (2021). "Quantile of a probability distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/quantile.
Most of the learning materials found on this website are now available in a traditional textbook format.