Tutorial: how to find the geometric multiplicity of an eigenvalue

The geometric multiplicity of an eigenvalue is the dimension of the linear space of its associated eigenvectors (i.e., its eigenspace).

You will find below a step-by-step tutorial that shows you how to find the geometric multiplicity of an eigenvalue with WolframAlpha, an incredibly useful web app that you can use as a linear-algebra calculator.

If you want to learn the theory in detail, you can visit our page on the Algebraic and geometric multiplicity of eigenvalues.

Table of contents

Step 1: open WolframAlpha in a new window
Step 2: find the eigenvalues of your matrix
Step 3: compute the RREF of the nilpotent matrix
Step 4: show your appreciation

Step 1: open WolframAlpha in a new window

We will use WolframAlpha as a calculator.

Follow this link to open WolframAlpha in a new window.

Step 2: find the eigenvalues of your matrix

The first thing to do is to find the eigenvalues of your matrix.

In this tutorial we are going to use the matrix [eq1] as an example.

In WolframAlpha, this matrix is written as {{1,0,2},{-1,1,3},{0,0,2}}. Copy this string in the WolframAlpha search box and hit Return.

WolframAlpha search box used to calculate the geometric multiplicity of an eigenvalue

Here is the result you get.

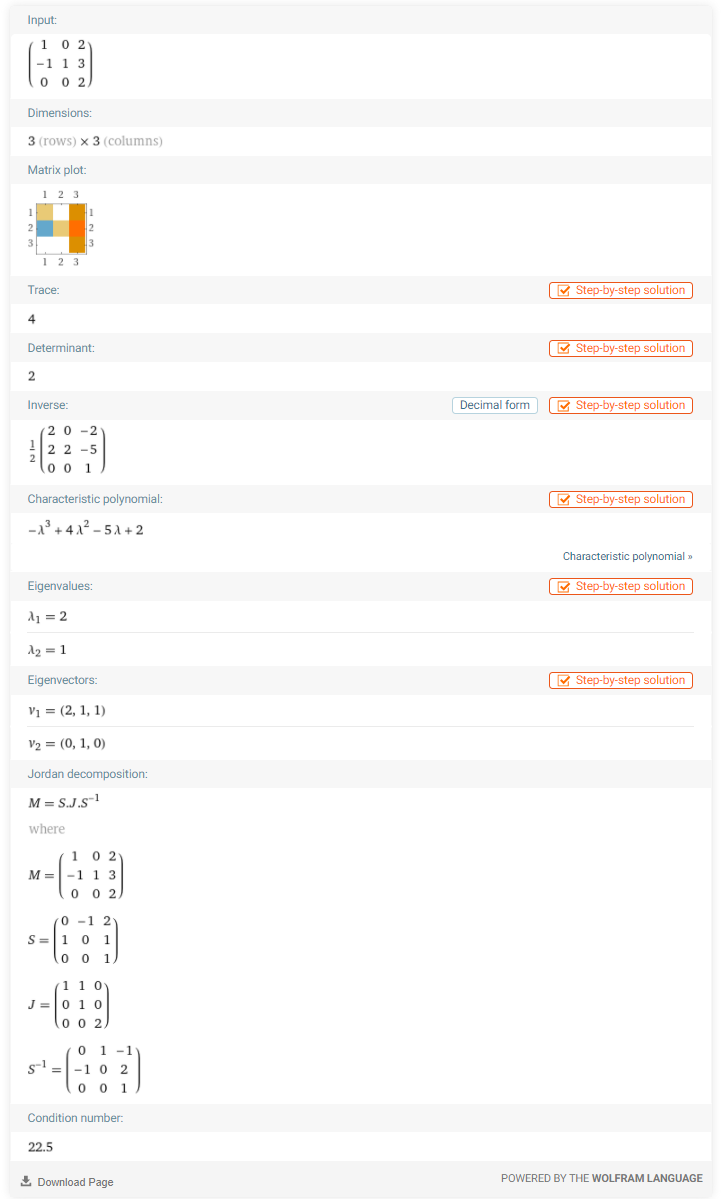
WolframAlpha results showing the Jordan form of the matrix

As you can see, the matrix has two eigenvalues: $lambda _{1}=2$ and $lambda _{2}=1$ .

If you know about Jordan forms, you will immediately be able to see that the eigenvalue $lambda _{1}=2$ is repeated only once on the main diagonal of the Jordan form [eq2] Hence, both the algebraic and geometric multiplicity of $lambda _{1}$ are equal to . Instead, the eigenvalue $lambda _{2}=1$ is repeated twice, which means that its algebraic multiplicity is equal to . Its geometric multiplicity is equal to the number of Jordan blocks associated to $lambda _{2}$ , which is equal to .

The general rule is: the geometric multiplicity of an eigenvalue is equal to the number of Jordan blocks associated to that eigenvalue.

Do not worry if you do not know about Jordan forms. In the next step, we are going to show how to find the geometric multiplicity without Jordan forms.

Step 3: compute the RREF of the nilpotent matrix

Let us focus on the eigenvalue $lambda _{2}=1$ .

We know that an eigenvector $x_{2}$ associated to $lambda _{2}$ needs to satisfywhere is the identity matrix.

The eigenspace of $lambda _{2}$ is the set of all such eigenvectors. Denote the eigenspace by $E_{2}$ . Then,

The geometric multiplicity of $lambda _{2}$ is the dimension of $E_{2}$ .

Note that $E_{2}$ is the null space of $A-lambda _{2}I$ .

By the rank-nullity theorem, the dimension of $E_{2}$ must bewhere is the range of $A-lambda _{2}I$ .

In other words, the geometric multiplicity can be found by calculating the dimension of the span of the columns of $A-lambda _{2}I$ .

But this can be easily done by computing the reduced row echelon form (rref) of $A-lambda _{2}I$ .

In WolframAlpha, the matrix $A-lambda _{2}I$ is written as {{1,0,2},{-1,1,3},{0,0,2}} - IdentityMatrix[3].

To compute its rref, copy the following string in the search box and press Enter:

reduced row echelon form: ({{1,0,2},{-1,1,3},{0,0,2}} - IdentityMatrix[3])

Here is the result you get.

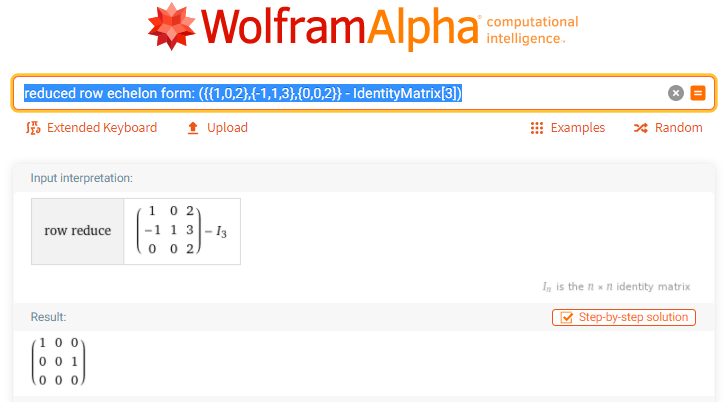
WolframAlpha result showing the reduced row echelon form of the nilpotent matrix

As you can see, the rref of $A-lambda _{2}I$ has two basic columns, which implies that

As a consequence, the geometric multiplicity of $lambda _{2}$ is

Step 4: show your appreciation

I guess we are done!

If you like this tutorial, please share this page with your friends, or link it from your blog.

How to cite

Please cite as:

Taboga, Marco (2021). "Tutorial: how to find the geometric multiplicity of an eigenvalue", Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/tutorial-how-to-find-geometric-multiplicity.