Jeffreys' scale

Jeffreys' scale of evidence is a subdivision of the possible values of the Bayes factor into categories (or grades).

The Bayes factor quantifies the strength of the evidence in favor of a model, as compared to another model.

Jeffreys' scale is used to translate the value of the Bayes factor into a qualitative judgement on the evidence (substantial, strong, very strong, etc.).

Table of contents

More than one scale
The Bayes factor
Jeffreys' original scale
Lee and Wagenmakers' scale
Kass and Raftery's scale
References

More than one scale

Statisticians use several different versions of Jeffreys' scale.

We report below three versions that are widely cited in the literature:

the original one, proposed by Jeffreys (1939);
a slight variation proposed by Lee and Wagenmakers (2014);
a more substantial modification by Kass and Raftery (1995).

The Bayes factor

Let be some data and $M_{1}$ and $M_{2}$ two models (i.e., two sets of probability distributions that could have generated the data).

Remember that the posterior odds ratio between $M_{1}$ and $M_{2}$ is

[eq1]

where [eq2] is the Bayes factor.

Values of the Bayes factor larger than are interpreted as evidence in favor of model $M_{1}$ (relative to $M_{2}$ ). The larger the values, the stronger the evidence.

On the contrary, values smaller than are interpreted as evidence in favor of $M_{2}$ .

Jeffreys' original scale

Here is Jeffreys' (1939) original scale.

B_1,2	log₁₀(B_1,2)	Grades of evidence
1 to 10^1/2	0 to 1/2	Barely worth mentioning
10^1/2 to 10	1/2 to 1	Substantial
10 to 10^3/2	1 to 3/2	Strong
10^3/2 to 10²	3/2 to 2	Very strong
> 10²	> 2	Decisive

Thus, the boundaries of the categories in Jeffreys' scale are $10^{n/2}$ for $n=0,\ldots ,4$ .

The grades above are for the evidence in favor of $M_{1}$ (values of the Bayes factor larger than ). When $B_{1,2}<1$ , we have categories of evidence in favor of $M_{2}$ , whose boundaries are the reciprocals of the boundaries in the previous table.

B_1,2	log₁₀(B_1,2)	Grades of evidence
1 to 10^-1/2	0 to -1/2	Barely worth mentioning
10^-1/2 to 10^-1	-1/2 to -1	Substantial
10^-1 to 10^-3/2	-1 to -3/2	Strong
10^-3/2 to 10^-2	-3/2 to -2	Very strong
< 10^-2	< -2	Decisive

For the sake of historical accuracy, here is the relevant excerpt from Jeffreys' book.

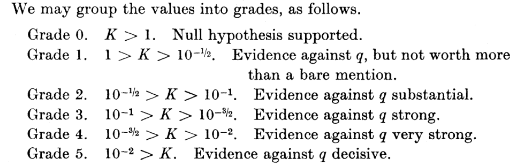
Excerpt from Jeffreys book where the grades of evidence are proposed.

Since the categories of evidence in favor of $M_{2}$ can be constructed mechanically from those in favor of $M_{1}$ , we do not report them for the other scales shown below.

Lee and Wagenmakers' scale

Lee and Wagenmakers (2014) made two minor modifications to Jeffreys' scale:

they rounded the two boundaries $10^{1/2}$ and $10^{3/2}$ to and respectively;
they changed the labels of the categories; in particular, they changed "substantial" to "moderate", as they thought that the original label sounded too decisive.

Here is the result of their changes.

B_1,2	Grades of evidence
1 to 3	Anecdotal
3 to 10	Moderate
10 to 30	Strong
30 to 100	Very strong
> 100	Extreme

Kass and Raftery's scale

Kass and Raftery (1995) simplified the scale by eliminating a category. Moreover, they raised the thresholds of strong and very strong evidence.

They also provided a logarithmic scale that is approximately equivalent to the ordinary scale.

B_1,2	2 ln(B_1,2)	Grades of evidence
1 to 3	0 to 2	Barely worth mentioning
3 to 20	2 to 6	Positive
20 to 150	6 to 10	Strong
> 150	> 10	Very strong

References

Jeffreys H. (1939) Theory of Probability, 3rd edition, Oxford University Press.

Lee M. D. and Wagenmakers, E.-J. (2014) Bayesian cognitive modeling: A practical course, Cambridge University Press.

Kass, R. E. and Raftery, A. E. (1995) Bayes factors, Journal of the American Statistical Association, 90, 773-795.

How to cite

Please cite as:

Taboga, Marco (2021). "Jeffreys' scale", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/Jeffreys-scale.