Search for probability and statistics terms on Statlect
StatLect
Index > Matrix algebra

Gram-Schmidt process

by , PhD

The Gram-Schmidt process (or procedure) is a sequence of operations that allow us to transform a set of linearly independent vectors into a set of orthonormal vectors that span the same space spanned by the original set.

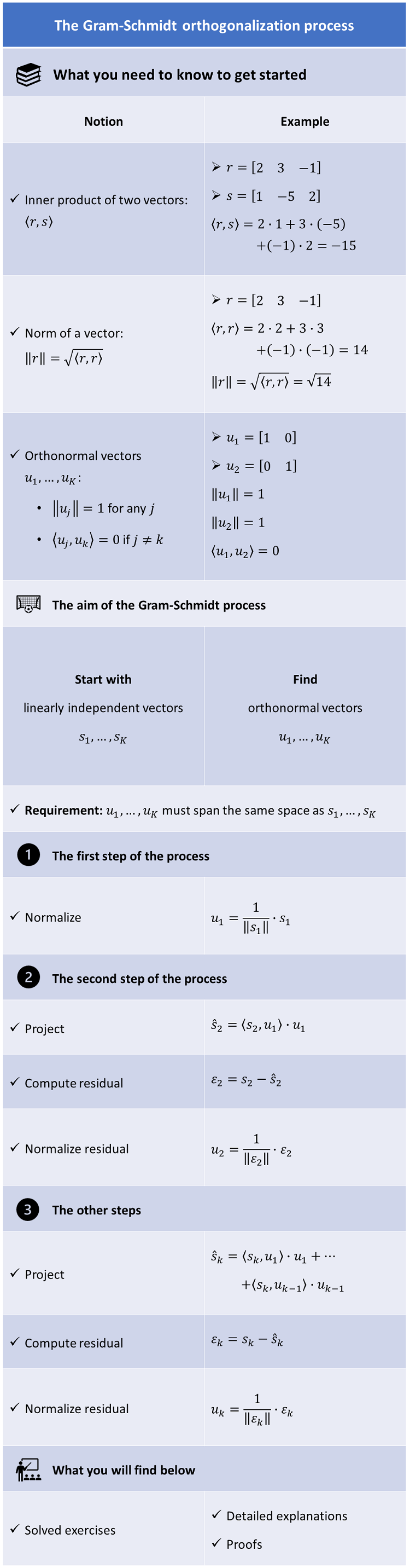
Infographic summarizing the main steps of the Gram-Schmidt orthogonalization algorithm.

Table of Contents

Preliminaries

Let us review some notions that are essential to understand the Gram-Schmidt process.

Remember that two vectors $r$ and $s$ are said to be orthogonal if and only if their inner product is equal to zero, that is,[eq1]

Given an inner product, we can define the norm (length) of a vector $s$ as follows:[eq2]

A set of vectors is called orthonormal if and only if its elements have unit norm and are orthogonal to each other. In other words, a set of K vectors [eq3] is orthonormal if and only if[eq4]

We have proved that the vectors of an orthonormal set are linearly independent.

When a basis for a vector space is also an orthonormal set, it is called an orthonormal basis.

Projections on orthonormal sets

In the Gram-Schmidt process, we repeatedly use the next proposition, which shows that every vector can be decomposed into two parts: 1) its projection on an orthonormal set and 2) a residual that is orthogonal to the given orthonormal set.

Proposition Let $S$ be a vector space equipped with an inner product [eq5]. Let [eq6] be an orthonormal set. For any $sin S$, we have[eq7]where $varepsilon _{S}$ is orthogonal to $u_{k}$ for any $k=1,ldots ,K.$

Proof

Define[eq8]Then, for each $j=1,ldots ,K$, we have that[eq9]where: in steps $frame{A}$ and $frame{B}$ we have used the fact that the inner product is linear in its first argument; in step $frame{C}$ we have used the fact that [eq10] if $k eq j$ since we are dealing with an orthonormal set; in step $frame{D}$ we have used the fact that the norm of $u_{j}$ is equal to 1. Therefore, $varepsilon _{S}$, as defined above, is orthogonal to all the elements of the orthonormal set, which proves the proposition.

The term[eq11]is called the linear projection of $s$ on the orthonormal set [eq12], while the term $varepsilon _{S}$ is called the residual of the linear projection.

Normalization

Another perhaps obvious fact that we are going to repeatedly use in the Gram-Schmidt process is that, if we take any non-zero vector and we divide it by its norm, then the result of the division is a new vector that has unit norm.

In other words, if [eq13] then, by the definiteness property of the norm, we have that [eq14]

As a consequence, we can define[eq15]and, by the positivity and absolute homogeneity of the norm, we have[eq16]

Overview of the procedure

Now that we know how to normalize a vector and how to decompose it into a projection on an orthonormal set and a residual, we are ready to explain the Gram-Schmidt procedure.

We are going to provide an overview of the process, after which we will express it formally as a proposition and we will discuss all the technical details in the proof of the proposition.

Here is the overview.

We are given a set of linearly independent vectors [eq17].

To start the process, we normalize the first vector, that is, we define[eq18]

In the second step, we project $s_{2}$ on $u_{1}$:[eq19]where $varepsilon _{2}$ is the residual of the projection.

Then, we normalize the residual:[eq20]

We will later prove that [eq21] (so that the normalization can be performed) because the starting vectors are linearly independent.

The two vectors $u_{1}$ and $u_{2}$ thus obtained are orthonormal.

In the third step, we project $s_{3}$ on $u_{1}$ and $u_{2}$:[eq22]and we compute the residual of the projection $varepsilon _{3}$.

We then normalize it:[eq23]

We proceed in this manner until we obtain the last normalized residual $u_{K} $.

At the end of the process, the vectors [eq24] form an orthonormal set because:

  1. they are the result of a normalization, and as a consequence they have unit norm;

  2. each $u_{k}$ is obtained from a residual that has the property of being orthogonal to [eq25].

To complete this overview, let us remember that the linear span of [eq17] is the set of all vectors that can be written as linear combinations of [eq17]; it is denoted by[eq28]and it is a linear space.

Since the vectors [eq29] are linearly independent combinations of [eq17], any vector that can be written as a linear combination of [eq17] can also be written as a linear combination of [eq29]. Therefore, the spans of the two sets of vectors coincide:[eq33]

Formal statement

We formalize here the Gram-Schmidt process as a proposition, whose proof contains all the technical details of the procedure.

Proposition Let $S$ be a vector space equipped with an inner product [eq5]. Let [eq35] be linearly independent vectors. Then, there exists a set of orthonormal vectors [eq36] such that[eq37]for any $kleq K$.

Proof

The proof is by induction: first we prove that the proposition is true for $k=1$, and then we prove that it is true for a generic k if it holds for $k-1$. When $k=1$, the vector[eq18]has unit norm and it constitutes by itself an orthonormal set: there are no other vectors, so the orthogonality condition is trivially satisfied. The set[eq39]is the set of all scalar multiples of $s_{1}$, which are also scalar multiples of $u_{1}$ (and vice versa). Therefore, [eq40]Now, suppose that the proposition is true for $k-1$. Then, we can project $s_{k}$ on [eq41]:[eq42]where the residual $varepsilon _{k}$ is orthogonal to [eq43]. Suppose that $varepsilon _{k}=0$. Then,[eq44]Since, by assumption, [eq45]for any $jleq k-1$, we have that [eq46]for any $jleq k-1$, where $alpha _{jl}$ are scalars. Therefore,[eq47]In other words, the assumption that $varepsilon _{k}=0$ leads to the conclusion that $s_{k}$ is a linear combination of [eq48]. But this is impossible because one of the assumptions of the proposition is that [eq17] are linearly independent. As a consequence, it must be that [eq50]. We can therefore normalize the residual and define the vector[eq51]which has unit norm. We already know that $varepsilon _{k}$ is orthogonal to [eq52]. This implies that also $u_{k}$ is orthogonal to [eq53]. Thus, [eq54] is an orthonormal set. Now, take any vector $sin S$ that can be written as[eq55]where [eq56] are scalars. Since, by assumption, [eq57]we have that equation (2) can also be written as[eq58]where [eq59] are scalars, and: in step $frame{A}$ we have used equation (1); in step $frame{B}$ we have used the definition of $u_{k}$. Thus, we have proved that every vector that can be written as a linear combination of [eq60] can also be written as a linear combination of [eq54]. Assumption (3) allows us to prove the converse in a completely analogous manner:[eq62]In other words, every linear combination of [eq54] is also a linear combination of [eq64]. This proves that [eq37]and concludes the proof.

Every inner product space has an orthonormal basis

The following proposition presents an important consequence of the Gram-Schmidt process.

Proposition Let $S$ be a vector space equipped with an inner product [eq5]. If $S$ has finite dimension [eq67], then there exists an orthonormal basis [eq68] for $S$.

Proof

Since $S$ is finite-dimensional, there exists at least one basis for $S$, consisting of K vectors [eq69]. We can apply the Gram-Schmidt procedure to the basis and obtain an orthonormal set [eq68]. Since [eq71] is a basis, it spans $S$. Therefore, [eq72]Thus, [eq29] is an orthonormal basis of $S$.

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Consider the space $S$ of all $3 imes 1$ vectors having real entries and the inner product[eq74]where $r,sin S$ and $s^{ op }$ is the transpose of $s$.

Define the vector[eq75]

Normalize $s$.

Solution

The norm of $s$ is[eq76]Therefore, the normalization of $s$ is[eq77]

Exercise 2

Consider the space $S$ of all $2 imes 1$ vectors having real entries and the inner product[eq78]where $r,sin S$ .

Consider the two linearly independent vectors[eq79]

Transform them into an orthonormal set by using the Gram-Schmidt process.

Solution

The norm of $s_{1}$ is [eq80]Therefore, the first orthonormal vector is[eq81]The inner product of $s_{2}$ and $u_{1}$ is[eq82]The projection of $s_{2}$ on $u_{1}$ is[eq83]The residual of the projection is[eq84]The norm of the residual is[eq85]and the normalized residual is[eq86]Thus, the orthonormal set we were looking for is[eq87]

How to cite

Please cite as:

Taboga, Marco (2021). "Gram-Schmidt process", Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

The books

Most of the learning materials found on this website are now available in a traditional textbook format.

Featured pages
Explore
Main sections
About
Glossary entries
Share
  • To enhance your privacy,
  • we removed the social buttons,
  • but don't forget to share.