The Student's t distribution is a continuous probability distribution that is often encountered in statistics (e.g., in hypothesis tests about the mean).
It arises when a normal random variable is divided by a Chi-square or a Gamma random variable.
Table of contents
Before going into details, we provide an overview.
A variable
has a standard Student's t distribution with
degrees of freedom if it can be written as a ratio
where:
has a standard normal distribution;
is a Chi-square random variable with
degrees of freedom;
and
are independent of each other.
A Chi-square variable with
degrees of freedom divided by
has a Gamma distribution (with parameters
and
).
As a consequence, we can also see a standard Student's t distribution with
degrees of freedom as a ratio
between
a standard normal variable and the square root of a Gamma variable
.
A variable
has a non-standard Student's t distribution if it can be
written as a linear transformation of a standard
one:
where
and
are defined as before.
The distribution is characterized by three parameters:
mean
;
scale
;
degrees of freedom
.
We start from the special case of the standard Student's t distribution.
By first explaining this special case, the exposition of the more general case is greatly facilitated.
The standard Student's t distribution is characterized as follows.
Definition
Let
be a continuous
random variable. Let its
support be the whole
set of real
numbers:
Let
.
We say that
has a standard Student's t distribution with
degrees
of freedom if and only if its
probability density
function
is
where
is a
constant:
and
is the Beta function.
Usually the number of degrees of freedom is integer
(),
but it can also be real
(
).
A standard Student's t random variable can be written as a normal random variable whose variance is equal to the reciprocal of a Gamma random variable, as shown by the following proposition.
Proposition
The probability density function of
can be written
as
where:
is the probability density function of a normal
distribution with mean
and variance
:
is the probability density function of a Gamma random variable with parameters
and
:
where
We need to prove
thatwhere
and
Let
us start from the integrand function:
where
and
is the probability density function of a random variable having a Gamma
distribution with parameters
and
.
Therefore:
![[eq23]](/images/student-t-distribution__53.png)
If
is a zero-mean normal random variable with variance
,
conditional on
,
then we can think of
as a
ratio
where
has a standard normal distribution,
has a Gamma distribution and
and
are independent.
The expected value of a standard Student's t random
variable
is well-defined only for
and it is equal
to
It follows from the fact that the density
function is symmetric around
:
![[eq26]](/images/student-t-distribution__67.png) The
above integrals are finite (and so the expected value is well-defined) only if
The
above integrals are finite (and so the expected value is well-defined) only if
because
and
the above limit is finite only if
.
The variance of a standard Student's t random
variable
is well-defined only for
and it is equal
to
It can be derived thanks to the usual
variance formula
()
and to the integral representation of the Beta
function:
![[eq30]](/images/student-t-distribution__75.png) From
the above derivation, it should be clear that the variance is well-defined
only when
From
the above derivation, it should be clear that the variance is well-defined
only when
.
Otherwise, if
,
the above improper integrals do not converge (and the Beta function is not
well-defined).
The
-th
moment of a standard Student's t random variable
is well-defined only for
and it is equal
to
By using the definition of moment, we
get![[eq32]](/images/student-t-distribution__82.png) Therefore,
to compute the
Therefore,
to compute the
-th
moment and to verify whether it exists and is finite, we need to study the
following
integral:
![[eq33]](/images/student-t-distribution__84.png) From
the above derivation, it should be clear that the
From
the above derivation, it should be clear that the
-th
moment is well-defined only when
.
Otherwise, if
,
the above improper integrals do not converge (the integrals involve the Beta
function, which is well-defined and converges only when its arguments are
strictly positive - in this case only if
).
Therefore, the
-th
moment of
is
A standard Student's t random variable
does not possess a moment generating
function.
When a random variable
possesses a moment generating function, then the
-th
moment of
exists and is finite for any
.
But we have proved above that the
-th
moment of
exists only for
.
Therefore,
can not have a moment generating function.
There is no simple expression for the characteristic function of the standard Student's t distribution. It can be expressed in terms of a Modified Bessel function of the second kind (a solution of a certain differential equation, called modified Bessel's differential equation).
The interested reader can consult Sutradhar (1986).
There is no simple formula for the
distribution function
of a standard Student's t random variable
because the
integral
cannot
be expressed in terms of elementary functions.
Therefore, it is usually necessary to resort to computer algorithms to compute
the values of
.
For example, the MATLAB
command:returns
the value of the distribution function at the point
x
when the degrees of freedom parameter is equal to n.
While in the previous section we restricted our attention to the Student's t distribution with zero mean and unit scale, we now deal with the general case.
The Student's t distribution is characterized as follows.
Definition
Let
be a continuous random variable. Let its support be the whole set of real
numbers:
Let
,
and
.
We say that
has a Student's t distribution with mean
,
scale
and
degrees
of freedom if and only if its probability density function
is
where
is a
constant:
and
is the Beta function.
We indicate that
has a t distribution with mean
,
scale parameter
and
degrees of freedom
by
To better understand the Student's t distribution, you can have a look at its density plots.
A random variable
has a t distribution with parameters
,
and
if it is a linear transformation of a standard Student's t
random variable.
Proposition
If
,
then
where
is a random variable having a standard t distribution.
Since
is strictly positive,
is a strictly increasing function of
.
Therefore, we can use the formula for the
density of a function of a continuous
variable:
The expected value of a Student's t random variable
is well-defined only for
and it is equal
to
It is an immediate consequence of the fact
that
(where
has a standard t distribution) and the linearity of the expected
value:
As
we have seen above,
is well-defined only for
and, as a consequence, also
is well-defined only for
.
The variance of a Student's t random variable
is well-defined only for
and it is equal
to
It can be derived using the formula for the
variance of affine transformations on
(where
has a standard t
distribution):
As
we have seen above,
is well-defined only for
and, as a consequence, also
is well-defined only for
.
A Student's t random variable
does not possess a moment generating function.
It is a consequence of the fact that
(where
has a standard t distribution) and of the fact that a standard
Student's t random variable does not possess a moment generating function
(see above).
There is no simple expression for the characteristic function of the Student's t distribution (see the comments above, for the standard case).
As in the case of the standard t distribution (see above), there is no simple
formula for the distribution function
of a Student's t random variable
.
As a consequence, it is usually necessary to resort to computer algorithms to
compute the values of
.
Most computer programs provide only routines for the computation of the
standard t distribution function (denote it by
).
In these cases we need to make a conversion, as
follows:For
example, the MATLAB
command:
returns
the value at the point
x of the distribution function
of a Student's t random variable with mean mu, scale
sigma and n degrees of
freedom.
The following sections contain more details about the t distribution.
A Student's t distribution with mean
,
scale parameter
and
degrees of freedom converges in distribution
to a normal distribution with mean
and variance
when the number of degrees of freedom
becomes large (converges to infinity).
As explained before, if
has a t distribution, it can be written
as
where
is a standard normal random variable, and
is a Chi-square random variable with
degrees of freedom, independent of
.
Moreover, as explained in the lecture on the
Chi-square distribution,
can be written as a sum of squares of
independent standard normal random variables
:
When
tends to infinity, the
ratio
converges
in probability to
,
by the Law of Large Numbers. As a consequence, by
Slutsky's theorem,
converges in distribution to
which
is a normal random variable with mean
and variance
.
As discussed above, if
has a standard normal distribution,
has a Gamma distribution with parameters
and
and
and
are independent, then the random variable
defined
as
has
a standard Student's t distribution with
degrees of freedom.
Given the same assumptions on
and
,
define a random variable
as
follows:
where
is a constant.
The variable
is said to have a non-central standard Student's t
distribution with
degrees of freedom and non-centrality parameter
.
We do not discuss the details of this distribution here, but be aware that this distribution is sometimes used in statistical theory (also in elementary problems) and that routines to compute its moments and its distribution function can be found in most statistical software packages.
This section shows the plots of the densities of some random variables having a t distribution.
The plots help us to understand how the shape of the t distribution changes by changing its parameters.
The following plot shows two Student's t probability density functions:
the blue line is the pdf of a Student's t random variable with parameters
,
and
;
the orange line is obtained by changing the parameters to
,
and
.
By changing only the mean, the shape of the density does not change, but the density is translated to the right (its location changes).
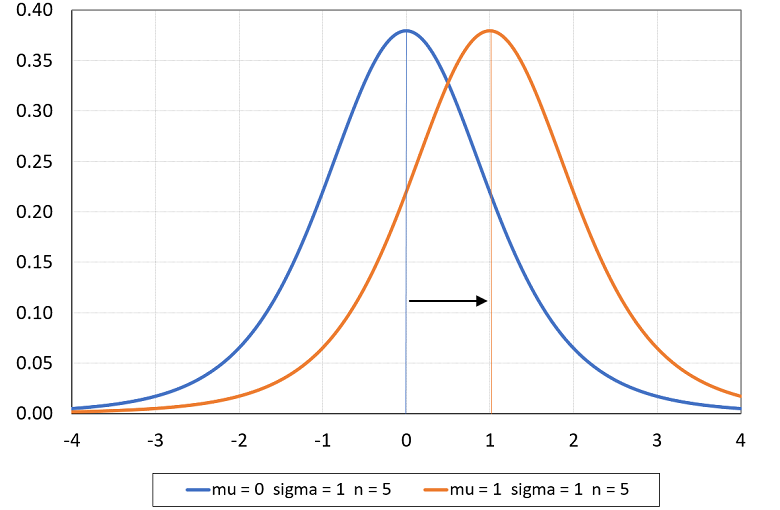
In the following plot:
the blue line is the pdf of a Student's t random variable with parameters
,
and
;
the orange line is obtained by changing the parameters to
,
and
.
By changing only the scale parameter, from
to
,
the location of the graph does not change (it remains centered at
),
but the shape of the graph changes (there is less density in the center and
more density in the tails).
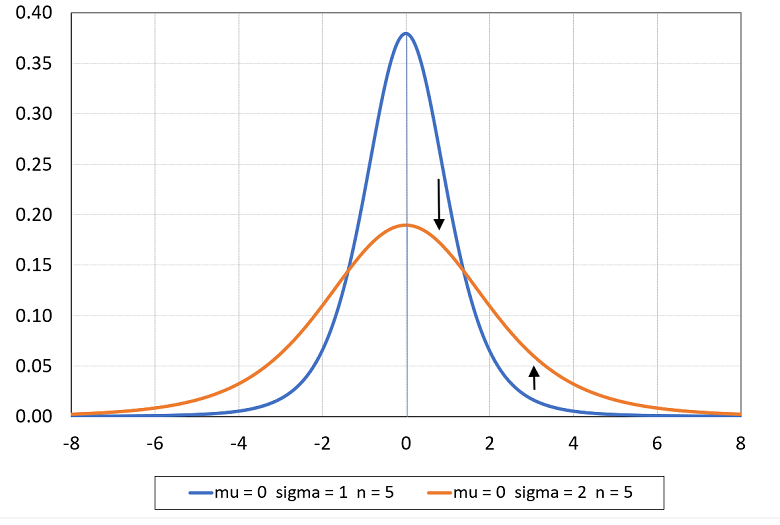
In the following plot:
the blue line is the pdf of a Student's t random variable with parameters
,
and
;
the orange line is obtained by changing the parameters to
,
and
.
By changing only the number of degrees of freedom, from
to
,
the location of the graph does not change (it remains centered at
)
and its shape changes only marginally (the tails become thinner).
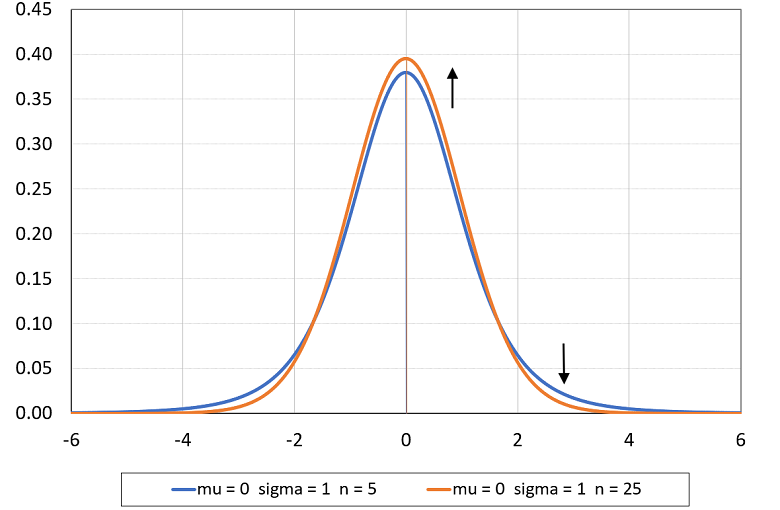
Below you can find some exercises with explained solutions.
Let
be a normal random variable with mean
and variance
.
Let
be a Gamma random variable with parameters
and
,
independent of
.
Find the distribution of the
ratio
We can
writewhere
has a standard normal distribution and
has a Gamma distribution with parameters
and
.
Therefore, the
ratio
has
a standard Student's t distribution with
degrees of freedom and
has a Student's t distribution with mean
,
scale
and
degrees of freedom.
Let
be a normal random variable with mean
and variance
.
Let
be a Gamma random variable with parameters
and
,
independent of
.
Find the distribution of the random
variable
We can
writewhere
has a standard normal distribution and
has a Gamma distribution with parameters
and
.
Therefore, the
ratio
has
a standard Stutent's t distribution with
degrees of freedom.
Let
be a Student's t random variable with mean
,
scale
and
degrees of freedom.
Compute
First of all, we need to write the
probability in terms of the
distribution function of
:
![[eq77]](/images/student-t-distribution__268.png) Then,
we express the distribution function of
Then,
we express the distribution function of
in terms of the distribution function of a standard Student's t random
variable
with
degrees of
freedom:
so
that:
where
the difference
can be computed with a computer algorithm, for example using the MATLAB
command
tcdf(0,6)-tcdf(-1/2,6)
Sutradhar, B. C. (1986) On the characteristic function of multivariate Student t-distribution, Canadian Journal of Statistics, 14, 329-337.
Please cite as:
Taboga, Marco (2021). "Student's t distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/student-t-distribution.
Most of the learning materials found on this website are now available in a traditional textbook format.