The multivariate (MV) Student's t distribution is a multivariate continuous distribution that generalizes the one-dimensional Student's t distribution.
Table of contents
Recall that a random variable has a standard univariate Student's t distribution if it can be represented as a ratio between a standard normal random variable and the square root of a Gamma random variable.
Analogously, a random vector has a standard MV Student's t distribution if it can be represented as a ratio between a standard MV normal random vector and the square root of a Gamma random variable.
This "standard" case is introduced in the next section, while the subsequent section deals with the more general case, that is, the case of random vectors that are obtained from linear transformations of standard multivariate Student vectors.
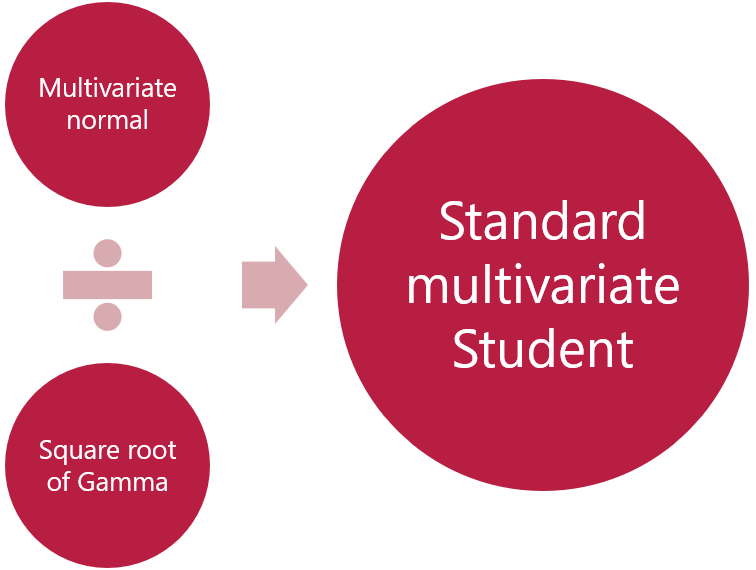
This section introduces the simpler, but less general, "standard" case.
Standard multivariate Student's t random vectors are characterized as follows.
Definition
Let
be a
continuous random
vector. Let its
support be the set
of
-dimensional
real
vectors:
Let
.
We say that
has a standard multivariate Student's t distribution with
degrees
of freedom if its
joint probability
density function
is
where
and
is the Gamma function.
When
,
the definition of the standard multivariate Student's t distribution coincides
with the definition of the standard univariate Student's t distribution.
This is proved as
follows:![[eq6]](/images/multivariate-student-t-distribution__12.png) The
latter is the probability density function of a standard univariate Student's
t distribution.
The
latter is the probability density function of a standard univariate Student's
t distribution.
A standard multivariate Student's t random vector can be written as a multivariate normal vector whose covariance matrix is scaled by the reciprocal of a Gamma random variable, as shown by the following proposition.
Proposition (Integral
representation)
The joint probability density function of
can be written
as
where:
is the joint probability density function of a
multivariate normal distribution with mean
and covariance
(where
is the
identity
matrix):
where
is the probability density function of a Gamma
random variable with parameters
and
:
where
We need to prove
thatwhere
and
We
start from the integrand function:
where
and
is the probability density function of a random variable having a Gamma
distribution with parameters
and
.
Therefore,
![[eq21]](/images/multivariate-student-t-distribution__35.png)
The marginal distribution of any one of the entries of
is a univariate standard Student's t distribution with
degrees of freedom.
Denote the
-th
component of
by
.
The marginal
probability density function of
is derived by integrating the joint probability density function with respect
to the other entries of
:
![[eq22]](/images/multivariate-student-t-distribution__43.png) where
where![]() is
the marginal probability density function of the entry of a multivariate
normal random vector with mean
is
the marginal probability density function of the entry of a multivariate
normal random vector with mean
and covariance
. This is equal to the density of a normal random
variable with mean
and variance
:
Therefore,
we have
that
But,
by the above proposition (Integral representation), this implies that
has a standard multivariate Student's t distribution with
degrees of freedom. Hence, it has a standard univariate Student's t
distribution with
degrees of freedom, because the two are the same thing when
.
The expected value of a standard multivariate
Student's t random vector
is well-defined only when
and it
is
Note
that
if
for all
components
.
But the marginal distribution of
is a standard Student's t distribution with
degrees of freedom. Therefore,
provided
.
The covariance matrix of a standard multivariate
Student's t random vector
is well-defined only when
and it
is
where
is the
identity matrix.
We have proved above that
.
This
implies
We
have also proved that
has a multivariate normal distribution with
mean
and
covariance
matrix
As
a
consequence,
and
![[eq37]](/images/multivariate-student-t-distribution__77.png) where
where
has been obtained as
follows:
![[eq39]](/images/multivariate-student-t-distribution__79.png)
This section deals with the general case.
Multivariate Student's t random vectors are characterized as follows.
Definition
Let
be a
continuous random vector. Let its support be the set of
-dimensional
real
vectors:
Let
be a
vector,
a
symmetric and positive definite matrix and
.
We say that
has a multivariate Student's t distribution with
mean
, scale
matrix
and
degrees
of freedom if its joint probability density function
is
where
We indicate that
has a multivariate Student's t distribution with mean
,
scale matrix
and
degrees of freedom
by
If
,
then
is a linear function of a standard Student's t random
vector.
Proposition
Let
.
Then,
where
is a
vector having a standard multivariate Student's t distribution with
degrees of freedom and
is a
invertible matrix such that
.
Because
is invertible, we have
that
is
a linear one-to-one mapping. Therefore, we can use the formula for the
joint density of a linear function of a
continuous random
vector:
![[eq50]](/images/multivariate-student-t-distribution__112.png) The
existence of a matrix
The
existence of a matrix
satisfying
is guaranteed by the fact that
is symmetric and positive definite.
The expected value of a multivariate Student's t random vector
is
This
is an immediate consequence of the fact that
(where
has a standard multivariate Student's t distribution) and of the linearity of
the expected
value:
The covariance matrix of a multivariate Student's t random vector
is
This
is an immediate consequence of the fact that
(where
has a standard multivariate Student's t distribution) and of the
Addition to constant vectors and
Multiplication by constant matrices properties
of the covariance
matrix:
![]()
Please cite as:
Taboga, Marco (2021). "Multivariate Student's t distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/multivariate-student-t-distribution.
Most of the learning materials found on this website are now available in a traditional textbook format.