Search for probability and statistics terms on Statlect
StatLect
Index > Probability distributions

F distribution

by , PhD

The F distribution is a univariate continuous distribution often used in hypothesis testing.

Table of Contents

How it arises

A random variable X has an F distribution if it can be written as a ratio[eq1]between a Chi-square random variable $Y_{1}$ with $n_{1}$ degrees of freedom and a Chi-square random variable $Y_{2}$, independent of $Y_{1}$, with $n_{2}$ degrees of freedom (where each variable is divided by its degrees of freedom).

Ratios of this kind occur very often in statistics.

Definition

F random variables are characterized as follows.

Definition Let X be a continuous random variable. Let its support be the set of positive real numbers:[eq2]Let [eq3]. We say that X has an F distribution with $n_{1}$ and $n_{2}$ degrees of freedom if and only if its probability density function is[eq4]where $c$ is a constant:[eq5]and $Bleft( {} ight) $ is the Beta function.

To better understand the F distribution, you can have a look at its density plots.

Relation to the Gamma distribution

An F random variable can be written as a Gamma random variable with parameters $n_{1}$ and $h_{1}$, where the parameter $h_{1}$ is equal to the reciprocal of another Gamma random variable, independent of the first one, with parameters $n_{2}$ and $h_{2}=1$.

Proposition The probability density function of X can be written as[eq6]where:

  1. [eq7] is the probability density function of a Gamma random variable with parameters $n_{1}$ and $frac{1}{z}$:[eq8]

  2. [eq9] is the probability density function of a Gamma random variable with parameters $n_{2}$ and $h_{2}=1$:[eq10]

Proof

We need to prove that[eq11]where[eq12]and[eq13]Let us start from the integrand function: [eq14]where [eq15]and [eq16] is the probability density function of a random variable having a Gamma distribution with parameters $n_{1}+n_{2}$ and [eq17]. Therefore,[eq18]

Relation to the Chi-square distribution

In the introduction, we have stated (without a proof) that a random variable X has an F distribution with $n_{1}$ and $n_{2}$ degrees of freedom if it can be written as a ratio[eq19]where:

  1. $Y_{1}$ is a Chi-square random variable with $n_{1}$ degrees of freedom;

  2. $Y_{2}$ is a Chi-square random variable, independent of $Y_{1}$, with $n_{2}$ degrees of freedom.

The statement can be proved as follows.

Proof

This statement is equivalent to the statement proved above (relation to the Gamma distribution): X can be thought of as a Gamma random variable with parameters $n_{1}$ and $h_{1}$, where the parameter $h_{1}$ is equal to the reciprocal of another Gamma random variable Z, independent of the first one, with parameters $n_{2}$ and $h_{2}=1$. The equivalence can be proved as follows.

Since a Gamma random variable with parameters $n_{1}$ and $h_{1}$ is just the product between the ratio $h_{1}/n_{1}$ and a Chi-square random variable with $n_{1}$ degrees of freedom (see the lecture entitled Gamma distribution), we can write [eq20]where $Y_{1}$ is a Chi-square random variable with $n_{1}$ degrees of freedom. Now, we know that $h_{1}$ is equal to the reciprocal of another Gamma random variable Z, independent of $Y_{1}$, with parameters $n_{2}$ and $h_{2}=1$. Therefore,[eq21]But a Gamma random variable with parameters $n_{2}$ and $h_{2}=1$ is just the product between the ratio $1/n_{2}$ and a Chi-square random variable with $n_{2}$ degrees of freedom. Therefore, we can write [eq22]

Expected value

The expected value of an F random variable X is well-defined only for $n_{2}>2$ and it is equal to[eq23]

Proof

It can be derived thanks to the integral representation of the Beta function:[eq24]

In the above derivation we have used the properties of the Gamma function and the Beta function. It is also clear that the expected value is well-defined only when $n_{2}>2$: when $n_{2}leq 2$, the above improper integrals do not converge (both arguments of the Beta function must be strictly positive).

Variance

The variance of an F random variable X is well-defined only for $n_{2}>4$ and it is equal to[eq25]

Proof

It can be derived thanks to the usual variance formula ([eq26]) and to the integral representation of the Beta function:[eq27]

In the above derivation we have used the properties of the Gamma function and the Beta function. It is also clear that the expected value is well-defined only when $n_{2}>4$: when $n_{2}leq 4$, the above improper integrals do not converge (both arguments of the Beta function must be strictly positive).

Higher moments

The k-th moment of an F random variable X is well-defined only for $n_{2}>2k$ and it is equal to[eq28]

Proof

It is obtained by using the definition of moment:[eq29]

In the above derivation we have used the properties of the Gamma function and the Beta function. It is also clear that the expected value is well-defined only when $n_{2}>2k$: when $n_{2}leq 2k$, the above improper integrals do not converge (both arguments of the Beta function must be strictly positive).

Moment generating function

An F random variable X does not possess a moment generating function.

Proof

When a random variable X possesses a moment generating function, then the k-th moment of X exists and is finite for any $kin U{2115} $. But we have proved above that the k-th moment of X exists only for $k<n_{2}/2$. Therefore, X can not have a moment generating function.

Characteristic function

There is no simple expression for the characteristic function of the F distribution.

It can be expressed in terms of the Confluent hypergeometric function of the second kind (a solution of a certain differential equation, called confluent hypergeometric differential equation).

The interested reader can consult Phillips (1982).

Distribution function

The distribution function of an F random variable is[eq30]where the integral[eq31]is known as incomplete Beta function and is usually computed numerically with the help of a computer algorithm.

Proof

This is proved as follows:[eq32]

Density plots

The plots below illustrate how the shape of the density of an F distribution changes when its parameters are changed.

Plot 1 - Increasing the first parameter

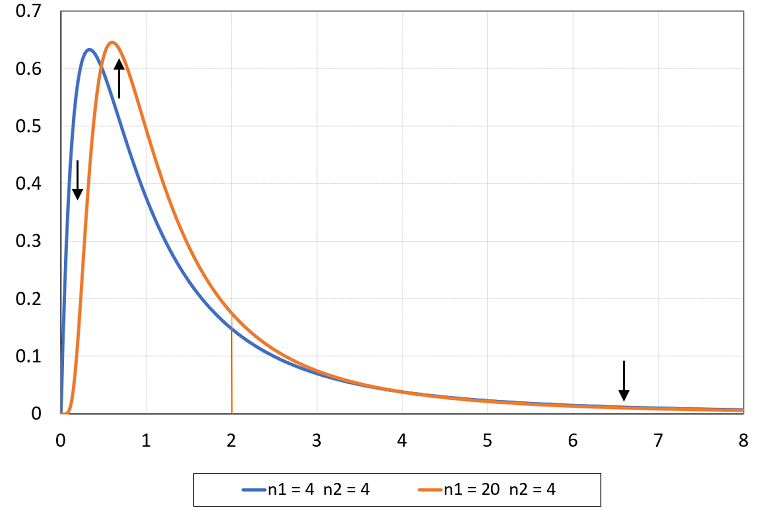
The following plot shows two probability density functions (pdfs):

By increasing the first parameter from $n_{1}=4$ to $n_{1}=20$, the mean of the distribution (vertical line) does not change.

However, part of the density is shifted from the tails to the center of the distribution.

F density plot 1

Plot 2 - Increasing the second parameter

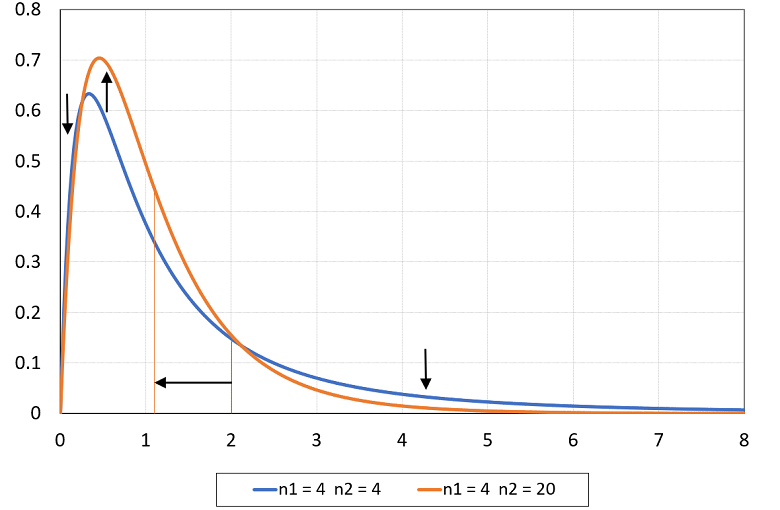
In the following plot:

By increasing the second parameter from $n_{2}=4$ to $n_{2}=20$, the mean of the distribution (vertical line) decreases (from $2$ to $frac{10}{9}$) and some density is shifted from the tails (mostly from the right tail) to the center of the distribution.

F density plot 2

Plot 3 - Increasing both parameters

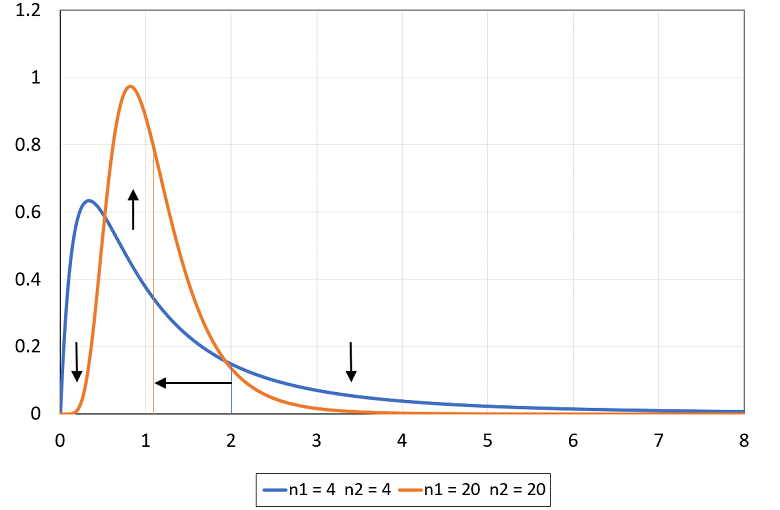
In the next plot:

By increasing the two parameters, the mean of the distribution decreases (from $2$ to $frac{10}{9}$) and density is shifted from the tails to the center of the distribution. As a result, the distribution has a bell shape similar to the shape of the normal distribution.

F density plot 3

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let X_1 be a Gamma random variable with parameters $n_{1}=3$ and $h_{1}=2 $.

Let X_2 be another Gamma random variable, independent of X_1, with parameters $n_{2}=5$ and $h_{1}=6$.

Find the expected value of the ratio[eq33]

Solution

We can write[eq34]where $Z_{1}$ and $Z_{2}$ are two independent Gamma random variables, the parameters of $Z_{1}$ are $overline{n}_{1}=3$ and $overline{h}_{1}=1$ and the parameters of $Z_{2}$ are $overline{n}_{2}=5$ and $overline{h}_{2}=1$ (see the lecture entitled Gamma distribution). By using this fact, the ratio can be written as[eq35]where $Z_{1}/Z_{2}$ has an F distribution with parameters $n_{1}=3$ and $n_{2}=5$. Therefore,[eq36]

Exercise 2

Find the third moment of an F random variable with parameters $n_{1}=6$ and $n_{2}=18$.

Solution

We need to use the formula for the k-th moment of an F random variable:[eq37]

Plugging in the parameter values, we obtain[eq38]where we have used the relation between the Gamma function and the factorial function.

References

Phillips, P. C. B. (1982) The true characteristic function of the F distribution, Biometrika, 69, 261-264.

How to cite

Please cite as:

Taboga, Marco (2021). "F distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/F-distribution.

The books

Most of the learning materials found on this website are now available in a traditional textbook format.

Featured pages
Explore
Main sections
About
Glossary entries
Share
  • To enhance your privacy,
  • we removed the social buttons,
  • but don't forget to share.